Para preparar la entrega de sus soluciones, cada participante elaborará una carpeta en algún servicio de nube (Google Drive, Dropbox, etc.) y deberá ajustar la configuración de esta carpeta para que cualquier persona con el link correspondiente pueda tener acceso a ella (esto con el objetivo de que los revisores tengan acceso a la misma). Este folder deberá contar con dos elementos principales:
1) Un archivo (formato PDF o MS-Word) con las respuestas finales a cada uno de los problemas,
2) Documentación que provea evidencias acerca de la manera como el participante obtuvo sus respuestas (es decir, hay que mostrar el trabajo realizado). Por ejemplo, cualquier código/programa que se haya escrito para que la computadora coadyuvara con los cálculos, o fotografías del papel/pizarrón en el cual el participante realizó cálculos a mano. El participante deberá cerciorarse de que los nombres de cada archivo permiten identificar con facilidad a qué problema corresponden.
La entrega de soluciones se realizará por medio del siguiente formulario:
en el cual el participante proporcionará dos datos: la cantidad de soluciones que se están entregando, y una liga a la carpeta en la nube que contiene tanto las respuestas finales, como las evidencias correspondientes.
*Cualquier modificación a los elementos de la carpeta posterior a la fecha límite de entrega invalidará de manera automática las respuestas del participante correspondiente.
1) (a) sean x_1,x_2,x_3 tres vectores distintos entre sí en (Z/3Z)^n tales que x_1=0 y x_2+x_3\neq 0. Sean y_1,y_2,y_3 otro conjunto de tres vectores distintos entre sí tales que y_1+y_2+y_3\neq 0. Demuestre que existe una transformación afín (es decir, una transformación lineal compuesta con una traslación) A tal que A(x_i)=y_i.
(b) Ahora considere los ocho vectores, en (Z/3Z)^3, dados por: x_1=(0,0,0) x_2=(1,1,0) x_3=(0,0,1) x_4=(1,1,1) y y_1=(0,0,0) y_2=(1,0,0) y_3=(0,1,0) y_4=(0,0,1)
Demuestre que no existe ninguna transformación afín que mande cada $x_i$ al correspondiente $y_i$.
2) Considere una cuadrícula S de enteros de tamaño m por n
S_{1,1} S_{1,2} ... S_{1,n} . . . . . . . . . S_{m,1} S_{m,2} ... S_{m,n}
Decimos que la entrada {i,j} en esta cuadrícula es "crítica" si S_{i,j} > 3.
Si una cuadrícula tiene al menos una entrada crítica, decimos que esta cuadrícula es "inestable", de lo contrario la llamamos "estable".
Si la entrada {i,j}-ésima de S es crítica, definimos una "operación de volcado" formando una nueva cuadrícula S' con entradas iguales a las de S, excepto S'{i,j} cuyo valor se obtiene restando 4 de S{i,j}, y sus vecinos superior, inferior, izquierdo y derecho, cuyos valores se obtienen aumentando en 1 sus valores originales. Si la entrada crítica no tiene todos los cuatro vecinos, aún así restamos 4 de su valor y aumentamos en 1 cada uno de los vecinos disponibles. De esta manera, S y S' diferirán como máximo en 5 entradas.
Demuestre que cualquier cuadrícula, después de un número finito de aplicaciones de operaciones de volcado, converge a una única cuadrícula estable, que llamamos su "estabilización". Demuestre que este número no depende de la elección del orden de las operaciones de volcado. Escriba un programa que tome como entrada una cuadrícula S de enteros no negativos y genere como salida 1) su estabilización S' y 2) el número de operaciones de volcado requeridos para llegar a S'
Ejemplos ("Entrada:" y "Salida:" sólo son encabezados y NO SON parte de la entrada y salida del programa)
Entrada:
2 2
2 4
Salida:
3 3
3 0
1
Entrada:
3 5 4 2
2 3 4 8
1 1 1 1
Salida:
2 2 1 2
1 0 2 3
2 3 3 3
13
3) Fijemos un número entero positivo n. Por una red entendemos un diagrama que consiste en cables y barras, como en la Figura 1.
Una n-coloreación admisible de la red es una asignación de una permutación a cada barra (cada barra actúa como un conector que permuta las hebras que la atraviesan) tal que • El diagrama resultante es una colección de n aros disjuntos (cada aro representa un color). • Ningún aro atraviesa la misma barra más de una vez. Una coloreación admisible queda completamente determinada por la elección de las permutaciones que reemplazan a las barras. Por ejemplo, consideremos la Figura 2, el ejemplo de la izquierda tiene la permutación identidad en cada barra y es una 4-coloreación admisible. Sin embargo, el ejemplo de la derecha no es una 3-coloreación admisible, ya que el aro externo atraviesa una barra más de una vez. Ejercicio: en la red de la Figura 3, • Encuentra las 6-coloreaciones admisibles. • Encuentra las 5-coloreaciones admisibles. (Cada coloración en su respuesta debe ser presentada en forma de dibujo.)
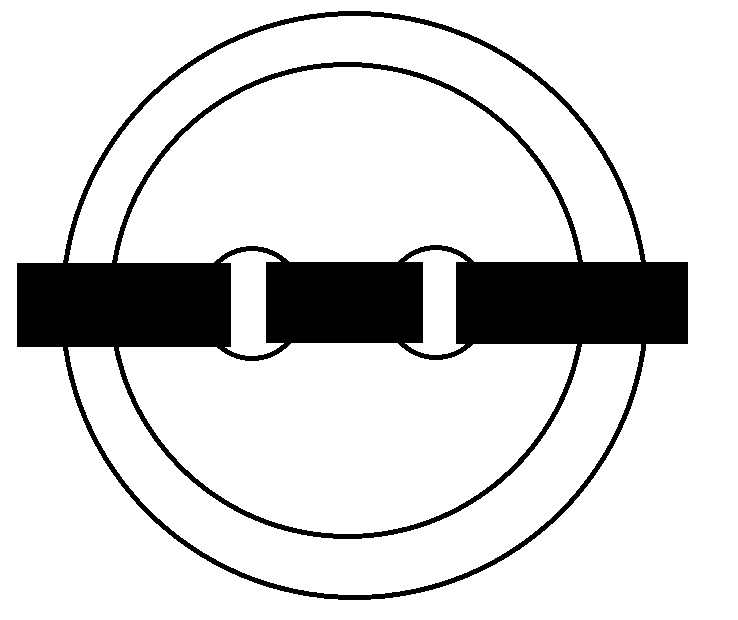
Figura 1
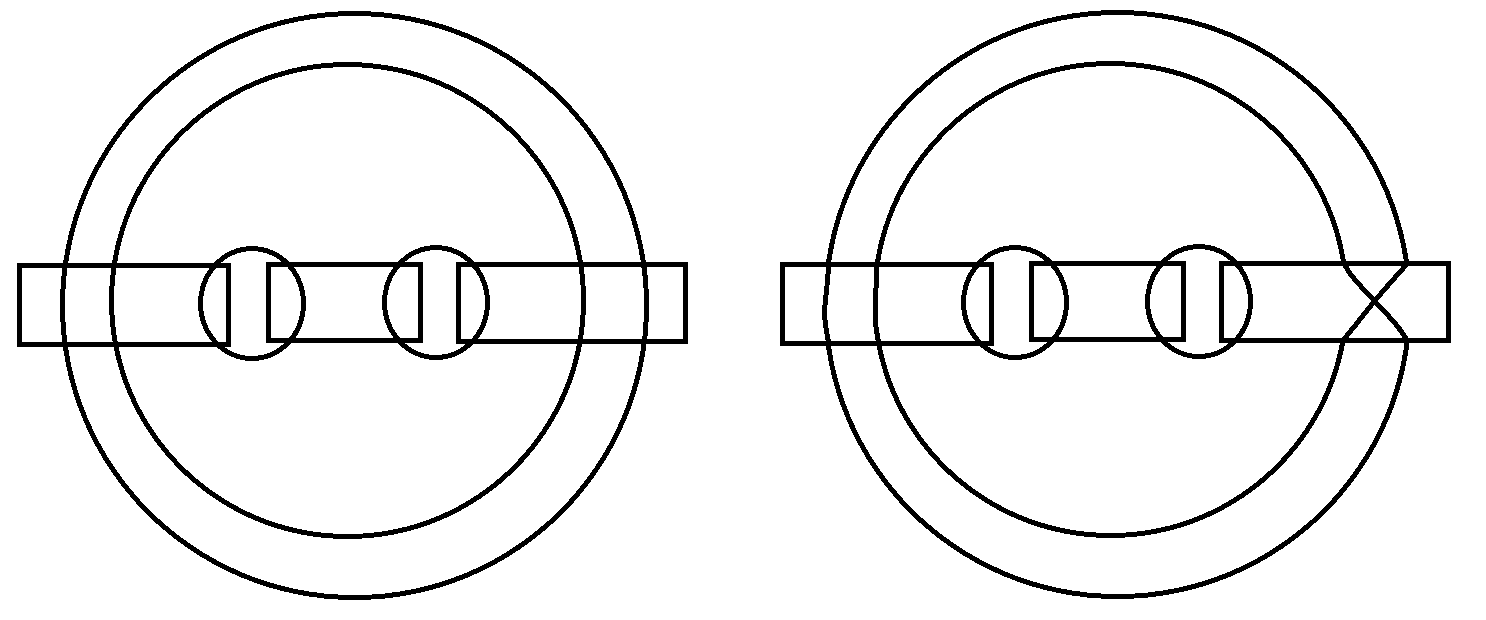
Figura 2
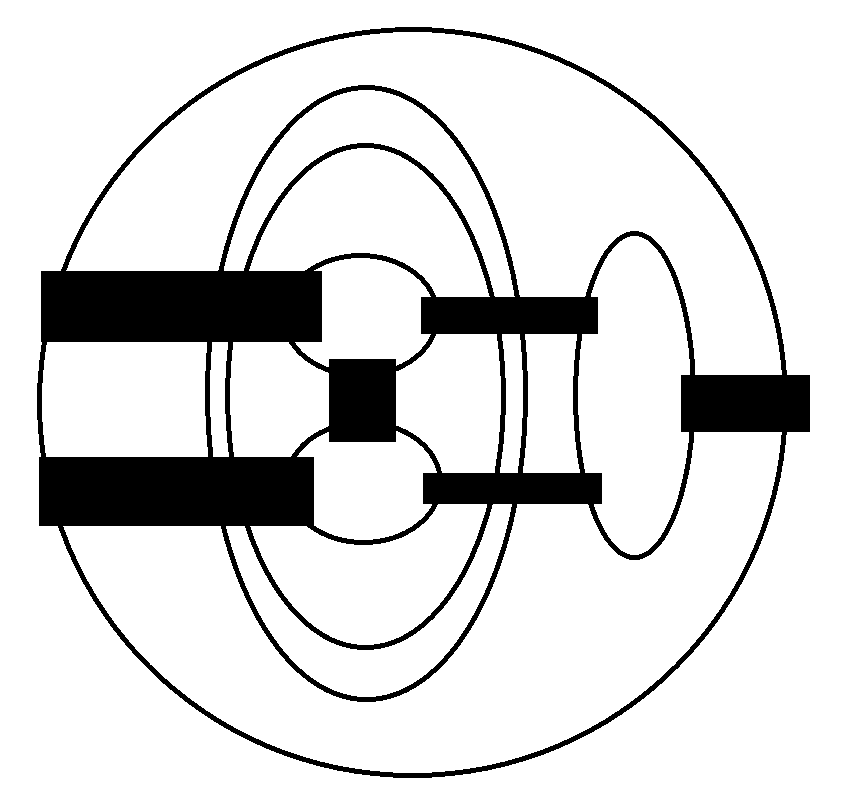
Figura 3
To submit solutions, each participant has to create a folder in some cloud service (Google Drive, Dropbox, etc.) and will have to adjust the settings of such folder so that anyone with the relevant link can view the folder (to ensure that the reviewers have access to it). This folder has to contain two main elements:
1) One file (either PDF or MS-Word format) with your final answers to each problem,
2) Documentation supporting what the participant did to obtain such answers (i.e. show your work!). For example, any code written to have the computer help with computations, or photographs of the paper/blackboard on which the participant performed computations by hand. Make sure you name files so that it is easy to identify which of the problems they correspond to.
To submit solutions, each participant will fill the following form:
In it, the participant will provide two pieces of information: the number of solutions submitted, and a link to the cloud folder containing both the final answers file and all supporting documentation.
Any modification to the cloud folder made after the submission deadline will automatically disqualify the participant.
1) (a) Let x_1,x_2,x_3 be three distinct vectors in (Z/3Z)^n such that x_1=0 and x_2+x_3\neq 0. Let y_1,y_2,y_3 be another set of three pairwise distinct vectors such that y_1+y_2+y_3\neq 0. Prove that there exists an affine transformation (that is, a linear transformation composed with a translation) A such that A(x_i)=y_i.
(b) Now consider the eight vectors in (Z/3Z)^3 given by: x_1=(0,0,0) x_2=(1,1,0) x_3=(0,0,1) x_4=(1,1,1) and y_1=(0,0,0) y_2=(1,0,0) y_3=(0,1,0) y_4=(0,0,1)
Prove that there is no affine transformation mapping each $x_i$ to the corresponding $y_i$.
2) Consider an m by n grid S of integers
S_{1,1} S_{1,2} ... S_{1,n} . . . . . . . . . S_{m,1} S_{m,2} ... S_{m,n}
We say that the {i,j}-th entry in this grid is "critical" if S_{i,j}>3.
If a grid has at least one critical entry, we say that this grid is "unstable", otherwise we call it "stable".
If the entry at {i,j} of S is critical, we define a "toppling" operation by forming a new grid S' with entries equal to entries of S, except S'{i,j} whose value is obtained by subtracting 4 from S{i,j}, and its up, down, left, and right neighbors, whose values are obtained by increasing their original values by 1. If a critical entry does not have all four neighbors, we still subtract 4 from its value and add 1 to each of the available neighbors. Thus S and S' will differ by at most 5 entries.
Show that any grid after a finite number of toppling applications converges to a unique stable grid, which we call its "stabilization". Show that this number does not depend on the choice of order of topplings. Write a program that takes as input a grid S of non-negative integers and 1) Outputs its stabilization S' and 2) Outputs the number of topplings required to arrive to S'.
Examples ("Input:" and "Output:" are headers and NOT part of the program's actual inputs or outputs)
Input:
2 2
2 4
Output:
3 3
3 0
1
Input:
3 5 4 2
2 3 4 8
1 1 1 1
Output:
2 2 1 2
1 0 2 3
2 3 3 3
13
3) Fix a positive integer n. By a net we mean a diagram consisting of cables and bars, such as Figure 1.
An admissible n-coloring of the net is a choice of permutation assignment to each bar (each bar acts as a connector that permutes strands passing through it) such that • The resulting diagram is a collection of n-disjoint loops (each loop represents a color). • No loop traverses the same bar more than once.
An admissible coloring is thus completely determined by the choice of permutations replacing the bars. For example, consider Figure 2, the left example has the identity permutation on each bar and it is an admissible 4-coloring. However, the right example is not an admissible 3-coloring, since the external loop passes through a bar more than once.
Exercise: in the net of Figure 3, • Find those admissible 6-colorings. • Find those admissible 5-colorings. (Each coloring in your answer must be presented as a picture.)
Figure 1
Figure 2
Figure 3
26 al 28 de mayo de 2025.
¿Qué es? Es un encuentro amistoso de programación, organizado por el IPN, la Universidad Nacional de Pusan (Corea del Sur), y la Universidad de Yonsei (Corea del Sur), aunque está abierto a la participación de alumnos de otras instituciones de licenciatura y posgrado.
¿Qué tipo de encuentro? El formato del encuentro consiste en que los participantes recibirán 3 problemas de ciencia de datos y matemáticas (cuya solución podría, o no, facilitarse enormemente por medio de la programación) y tendrán 3 días para resolverlos; al final de este período, deberán enviar sus respuestas.
El comité organizador decidirá cuáles respuestas son las mejores, para de este modo designar a un(a) ganador(a) por país.
Temática: Las matemáticas de la ciencia de datos.
Inscripciones: Deberán realizarse llenando el siguiente formulario: https://forms.gle/7kNLxNCXHgJz6AXv5
Fecha límite para inscribirse: 24 de mayo de 2025
Logística de la participación en el evento: Los tres problemas a resolver se publicarán el día 26 de mayo a las 6:00 PM (hora de México), equivalentemente a las 9:00 AM (hora de Corea), en esta página web.
La fecha límite para la entrega de sus soluciones será 72 horas después de la publicación de los problemas.
La entrega de soluciones se realizará por medio de un formulario de Google, en el cual el participante deberá indicar cuántos de los problemas resolvió, así como un link a alguna carpeta en la nube (Google Drive, Dropbox, etc.), la cual deberá de contener un archivo con las respuestas finales, así como los archivos con la evidencia de cómo obtuvo sus respuestas (esta puede ser una foto de los cálculos realizados, el código de algún programa que hayan escrito, etc.).
Para calificar sus soluciones, el comité organizador prestará atención tanto a las respuestas finales, como a la evidencia de los métodos utilizados para llegar a ellas.
Fecha límite para inscribirse: 24 de mayo de 2025
Ceremonia de premiación: -----
May 27-29, 2025.
What is this? A programming scrimmage organized by Pusan National University, Yonsei University, and Instituto Politécnico Nacional (Mexico), but open to participation of students from other undergraduate and graduate institutions.
What kind of scrimmage? Participants will receive 3 problems about mathematics and data science (whose solution may or may not be made easier by some judicious use of programming) and will be given 3 days to solve them; at the end of this period, they will submit their solutions.
The organizing committee will choose the best solutions in order to award one winner per country.
Theme: The mathematics of data science.
Registration: By filling out the following form: https://forms.gle/7kNLxNCXHgJz6AXv5
Deadline for registration: May 24, 2025
Logistics of participating: The three problems will be posted on May 27th, at 9:00 AM (Korea), or equivalently at 6:00 PM (Mexico), in this website.
The deadline for submitting solutions is 72 hours after the problems are posted.
Solutions submission will be made by filling out a form, in which the participant will input the number of problems that (s)he solved, as well as a link to a folder in the cloud (Google Drive, Dropbox, etc.); said folder must contain one file with all of the final answers, as well as additional files with evidence for how the problem was solved (photographs of your calculations by hand, any code you wrote, etc.).
In order to grade the solutions, the organizing committe will not only take into account the final answers, but also the approach to arrive at such answers, as shown in the evidence submitted.
Deadline for registration: May 24, 2025
Award ceremony: ------
INSTITUTO POLITÉCNICO NACIONAL
D.R. Instituto Politécnico Nacional (IPN). Av. Luis Enrique Erro S/N, Unidad Profesional Adolfo López Mateos, Zacatenco, Alcaldía Gustavo A. Madero, C.P. 07738, Ciudad de México. Conmutador: 55 57 29 60 00 / 55 57 29 63 00.
Esta página es una obra intelectual protegida por la Ley Federal del Derecho de Autor, puede ser reproducida con fines no lucrativos, siempre y cuando no se mutile, se cite la fuente completa y su dirección electrónica; su uso para otros fines, requiere autorización previa y por escrito de la Dirección General del Instituto.
